板橋村だより

上記の広告は、30日以上更新がないブログに表示されています。
新たに記事を投稿することで、広告を消すことができます。  

　
　
　
　Lorentz und Einstein photographiert
　von Ehrenfest vor seinem Haus in Leiden.　

　（旧暦　 6月 16日）

　数学セミナー(13)－相対性理論(4)－特殊相対性理論(4)のつづき

　互いに一定の早さvで相対運動している2つの慣性系 Ｋ ( x, y, z, t ) とＫ' ( x', y', z', t' )において、慣性系 ＫとＫ'の空間座標の原点が一致した瞬間を原点、t = t' = 0として、このときに原点から放射された光が真空中を伝わる速さはどの系においても同じだから、Ｋ ( x, y, z, t )系 とＫ' ( x', y', z', t' )系の ｔ および t' 秒後の光の分布は、それぞれ球面方程式より、下記のように表現されます。

　　

　ローレンツ変換とは、互いに一定の早さvで相対運動している2つの慣性系 Ｋ ( x, y, z, t ) とＫ' ( x', y', z', t' ) の関係式を求めること、つまり、Ｋ 系からＫ' 系への変換を求めることになりますが、これは数学的には、次式の各係数a～qを求める作業となります。

　　

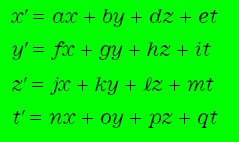
　　ここで、Ｋ' 系のｘ' 軸がＫ 系のｘ 軸の正の方向に速さｖ で運動しているとすると、ｔ 秒後のＫ' 系の原点 ｘ'＝0の地点は、Ｋ 系では ｘ＝ｖｔ となるから、ｘ' は次式で表されます。

　　

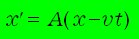
　また、Ｋ' 系はｘ 軸方向にだけ運動していることから ｙ' 式と ｚ' 式の ｔ の係数は0　となる必要があり、ｙ' 式と ｚ' 式および t' 式は次式のように省略できます。

　　  続きを読む

　

　蒲生野猟遊　　蒲生野は近江国湖東地方、蒲生郡域平野部の古称

　（旧暦　 6月 9日）

　天皇（すめらみこと）の蒲生野（かまふの）に遊猟（みかり）したまふ時、額田王の作る歌

　あかねさす紫野行き標野（しめの）行き　野守は見ずや君が袖振る　（巻1-20）

　皇太子（ひつぎのみこ）の答へましし御歌　
　明日香宮ニ御宇（あめのしたしらしめ）シシ天皇（すめらみこと）、諡シテ天武天皇トイフ

　紫のにほへる妹を憎くあらば　人妻ゆゑに吾（あれ）戀ひめやも　（巻1-21）

　紀ニ曰ハク、天皇七年丁卯、夏五月五日、蒲生野ニ縦猟（かり）シタマフ。時ニ大皇弟（ひつぎのみこ）諸王（おほきみたち）内臣（うちつまへつきみ）及ビ群臣（まへつきみたち）、皆悉（ことごと）ニ従（おほみとも）ソトイヘリ。


　日本書紀巻第二十九の天武天皇二年（673）二月癸未（27日）の記述に、

　『天皇（すめらみこと）初め鏡王の女（むすめ）額田姫王（ぬかたのひめみこ）を娶（めと）る。十市皇女を生む。』

　とありますが、額田王（ぬかだのおおきみ）は、はじめは大海人皇子（おおあまのみこ：後の天武天皇）に婚（みあ）い、十市皇女（とおちのひめみこ）を生みましたが、後に大海人皇子の兄である葛城皇子（かつらぎのみこ：中大兄皇子）に召されて宮中に侍していた、つまり、下々の者にはよくわかりませんが、まあ、そういう関係にあったということらしいです。

　この歌に関しては、かの斎藤茂吉先生（1882～1953）はその名著『万葉秀歌』の中で、

　この歌は、額田王が皇太子大海人皇子にむかい、対詠的にいっているので、濃やかな情緒に伴う、甘美な媚態をも感じ得るのである。（中略）　一首は平板に直線的ではなく、立体的波動的であるがために、重厚な奥深い響を持つようになった。云々・・
　
　などと、よく訳のわからない注釈を残しています。  続きを読む

　　

　Albert Einstein in 1904.

　（旧暦　 6月 3日）

　数学セミナー(12)－相対性理論(3)－特殊相対性理論(3)のつづき


　ローレンツ変換は、アインシュタインが考えた「光速度が慣性系によらず一定」であることから導く簡単な方法があります。

　ここで慣性系（かんせいけい）とは、『慣性の法則』が成立する座標系であり、『慣性の法則』とは

　『静止している質点は、力を加えられない限り、静止を続ける。運動している質点は、力を加えられない限り、等速直線運動を続ける。』　

というものです。

　1900年に卒業したスイスのチューリッヒ連邦工科大学（Eidgenössische Technische Hochschule, ETH）に助手として残ることもできず、かといって博士号も持たず、臨時の代理教員や家庭教師のアルバイトで収入を得ていた無名の青年は、1902年、友人の父親の口利きでベルンのスイス特許庁に3級技術専門職（審査官）として就職することができました。

　1905年、彼は博士号を取得するために、“Zur Elektrodynamik bewegter Körper” （運動している物体の電気力学）という論文を母校のチューリッヒ連邦工科大学に提出しますが、受け入れられませんでした。しかし、この「特殊相対性理論」に関連する最初の論文は、ドイツの学術誌『Annalen der Physik』 第17巻 pp.891～921 に掲載されました。

　§2. Über die Relativität von Längen und Zeiten.
　Die folgenden Überlegungen stüｔzen sich auf das Relativitätsprinzip und auf das Printzip der Konstanz der Lichtgeschwindigkeit, welche beiden Prinzipien wir folgendermaßen definieren.
　
　1.　Die Gesetze, nach denen sich die Zustände der physikalischen Systeme ändern, sind unabhängig davon, auf welches von zwei relativ zueinander in gleichförmiger Translationsbewegung befindlichen Koordinatensystemen diese Zustandsänderungen bezogen warden.

　2.　Jeder　Lichtstrahl bewegt sich im „ruhenden“ Koordinatensysytem mit der bestimmten Geschwindigkeit V, unabhängig davon, ob dieser Lichtstrahl von einem ruhenden oder bewegten Körper emittiert ist. Hierbei ist
　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　Geschwindigkeit ＝　Lichtweg／Zeitdauer ,

wobei „Zeitdauer“ im Sinne der Definition des §1 aufzufassen ist.  続きを読む

　

　葛飾北斎「冨嶽三十六景 武州千住」　by Wikipedia

　（旧暦　 5月28日）

　しばらくボ～～としておりましたら五月も二十八日（旧暦）になり、芭蕉翁一行は昨日は、出羽の国、立石寺の山上の堂にのぼって、「閑さや・・」などと一句詠んだことでしょう。

　さて、随行した門人曾良の「奥の細道随行記」によれば、日の出ころ深川を船で出立した一行は、「巳ノ下尅」つまり午前11時半ころ、千住大橋の北側付近で船を下りました。
　千住は日光街道第一の宿駅で、東海道品川宿、我が中山道板橋宿、甲州街道内藤新宿と並んで江戸四宿の１つに数えられていました。後の元禄8年（1695）には宿場の事務を取りまとめる「問屋場」が設置され、寛保3年（1743）には公用荷物を伝馬で運ぶための重量を測り運賃を決める役所である「貫目改所」が同じ敷地内に併設されています。

　千住から陸路で出発した芭蕉翁一行は、日光街道第二の宿駅草加を過ぎて、その日は江戸から9里（約36㎞）の粕壁（春日部）に宿泊しました。
　翌廿八日、「辰上剋」（午前7時半頃）、雨が止んだので宿を出て栗橋の関所を通過し、その日は粕壁より9里の間々田（小山市）に宿泊しています。
　廿九日、「辰上剋」（午前7時半頃）間々田の宿を出て、この日は「けむり」の歌枕の名所である室の八島（栃木市惣社町）に詣でました。

　ここで随伴の曾良が云うには、室の八島の神は木の花さくや姫といって富士山本宮浅間神社の神と一躰であるとのこと。
　
　木の花さくや姫の故事は、日本書紀巻第二神代［下］に記述されています。

　天照大神（あまてらすおおみかみ）の孫の瓊瓊杵尊（ににぎのみこと）が下界を治めるために高天原から日向の高千穂の峰に天降りますが、そののち、瓊瓊杵尊（ににぎのみこと）は笠沙の御崎(鹿児島県野間半島)で出会った美しい鹿葦津姫（木花之開耶姫）と結ばれます。  続きを読む

　

　円山應擧筆 『張子房圖』　by Wikipedia
　張良、字は子房。漢の高祖劉邦に仕えて軍師として活躍し、漢の創業を助けた。蕭何、韓信と共に劉邦配下の三傑とされ、高祖劉邦より留（江蘇省徐州市沛県の東南）に領地を授かったので留侯とも呼ばれる。
　謀（はかりごと）を帷帳の中に回らし、勝つことを千里の外に決せし者なり

　（旧暦　 5月26日）

　鷗外忌　石見人森林太郎の大正11年（1922）の忌日。 　

　漢詩（16）－文天祥（1）－正氣の歌（1）のつづき

　天地有正氣　　天地に正氣あり
　雜然賦流形　　雜然として流形を賦す
　下則爲河嶽　　下れば則ち河嶽と爲り
　上則爲日星　　上れば則ち日星と爲る
　於人曰浩然　　人に於いては浩然と曰ひ
　沛乎塞蒼冥　　沛乎として蒼冥に塞（み）つ
　皇路當淸夷　　皇路淸夷に當れば
　含和吐明庭　　和を含み明庭に吐く
　時窮節乃見　　時窮（きはま）らば節乃ち見（あらは）れ
　一一垂丹靑　　一一丹靑に垂る

　天地には正気（せいき）があり
　混然として形を持たずこの世界にある
　下に行けば河や山岳と為り
　上に行けば日星と為る
　人に於いて浩然の気と言い
　大いに天地に満ちている
　政治の大道が清く治まっておれば
　その結果が朝廷のまつりごとにも出てくる
　動乱の時代になれば、正気を元とした節義が顕れ
　一つ一つ史書に残る

　在齊太史簡　齊に在りては太史の簡
　在晉董狐筆　晉に在りては董狐の筆
　在秦張良椎　秦に在りては張良の椎（つい）
　在漢蘇武節　漢に在りては蘇武の節  続きを読む

　

　東京海洋大学越中島キャンパス構内の明治丸

　（旧暦　 5月23日）

　照りもせぬ曇りもせぬ　春のおぼろ月
　いたずらに去り行く　人生の春を嘆く
　乙女ならずも耳を傾けて　聞くであろう
　さらば歌わん我等が唄を　白菊の歌
　
　かすめるみ空に消えのこる おぼろ月夜の秋の空
　身にしみわたる夕風に 背広の服をなびかせつ

　紅顔可憐の美少年が 商船学校の校内の
　練習船のメンマスト トップの上に立ち上り

　故郷の空を眺めつつ ああ父母は今いずこ
　我が恋人は今いかに 少年左手（ゆんで）に持つものは

　月の光に照らされて 傍（かたえ）の友に語るよう
　もとこのものは故郷（ふるさと）の 外山（とやま）のかげに咲き残る

　後（おく）れ咲きたる白菊を 吾れ故郷（ふるさと）を出（い）づる時
　君が形見と贈られし 真心こめしこのしおり

　海山遠くへだつとも 彼が形見を思い出（い）で
　朝な夕なにながめつつ いわんとすれど悲しやな

　（旧商船学校　白菊の歌）

　旧商船学校の白菊の歌は有名な歌で、私「嘉穂のフーケモン」も若かりし頃あこがれて歌っておりましたが、お袋から「商船学校だけはだめだ」と大反対され、やむなく札幌の農学校に進路を変更した懐かしい思い出があります。  続きを読む