2014年04月23日
漢詩(31)−陸游(1)−釵頭鳳

陸游(1125〜1210)
(旧暦3月24日)
釵頭鳳 陸游 釵頭鳳(さいとうほう) 陸游
紅酥手 紅酥(こうそ)の手
黄縢酒 黄縢(わうとう)の酒
滿城春色宮牆柳 滿城の春色 宮牆(きうしやう)の柳
東風惡 東風 惡しく
歡情薄 歡情 薄(はかな)し
一懷愁緒 一懷の愁緒
幾年離索 幾年の離索ぞ
錯 錯 錯 錯(あやま)てり 錯てり 錯てり
春如舊 春は舊(もと)の如く
人空痩 人は空しく痩せ
泪痕紅浥鮫綃透 泪痕紅く浥(うるほ)して鮫綃に透る
桃花落 桃花 落ち
閑池閣 閑かなる池閣
山盟雖在 山盟在りと雖も
錦書難托 錦書は托し難し
莫 莫 莫 莫(な)し 莫し 莫し

うすくれないの柔き手に
黄色き紙の封じ酒
城内一面春景色 宮壁沿いの若柳
春風悪しく
歓び儚(はかな)し
胸に抱きし淋しき思ひ
離別せしより幾年ぞ
ああ 錯(あやま)てり 錯てり 錯てり
春は昔のままなるも
人は空しくやせ衰へり
泪紅く頬つたい 手巾に滲みて散りにじむ
桃花は落ちて 閑かなる
池のほとりの楼閣に
深き契りはありとても
想いの文は出し難し
ああ 莫(な)かれ 莫かれ 莫かれ
「釵頭鳳」とは、六十文字からなる一種の詩歌の形式で、劇中で歌われる詩歌でした。しかし単に釵頭鳳というと、南宋の文人政治家、陸游(1125〜1210)と最初の妻、唐琬の釵頭鳳を指すほど有名です。
陸游は、南宋の高宗紹興十四年(1144)甲子、20歳の時に、母、唐氏の姪である唐琬と結婚し、仲睦まじく暮らしていましたが、妻と姑の唐氏との折り合いが悪く、一年ほどで離縁させられてしまいます。
しかし、高宗紹興二十五年(1155)乙亥、陸游31歳の時に、その別れた妻と沈家の庭園「沈園」で、偶然にも再開してしまいます。
沈園で出会った後、陸游はその激情をこの詞に託して沈園の壁に書いたと云われています。翌年、沈園を再訪した唐琬はこの詞を知り、彼女も詞を和して応えたとか。
「釵頭鳳」の形式は、次のようになっています。
○○●(韻)
○○●(韻)
●○○●○○●(韻)
○○●(韻)
○○●(韻)
●●○○
●○○●(韻)
●(韻)●(韻)●(韻)
○○●(韻)
○○●(韻)
●○○●○○●(韻)
○○●(韻)
○○●(韻)
●●○○
●○○●(韻)
●(韻)●(韻)●(韻)
釵頭鳳 唐琬 釵頭鳳 唐琬
世情薄 世情は薄く
人情惡 人の情は惡し
雨送黃昏花易落 雨 黃昏(たそがれ)を送り 花落ち易く
曉風干 曉風(げうふう)干き
泪痕殘 泪痕を殘す
欲箋心事 心事を箋(せん)に欲せんとし
獨語斜欄 獨語し欄に斜す
難 難 難 難(かた)し 難し 難し
人成各 人各々に成り
今非昨 今は昨(きのふ)に非ず
病魂常似鞦韆索 病魂 常に鞦韆(しうせん)の索に似たり
角聲寒 角聲寒く
夜闌珊 夜 闌珊(らんさん)たり
怕人尋問 人の尋問を怕(おそ)れ
咽淚裝歡 咽淚せしも歡を裝ふ
瞞 瞞 瞞 瞞(あざむ)かん 瞞かん 瞞かん

世情は薄く
情は悪(わる)し
雨は黃昏(たそがれ)を送り 花落ち易く
明けの風は 涙を乾かし
その痕を残す
心の想いを手紙に書かんと
一人つぶやき 手摺りに依るも
ああ できない できない できない
人それぞれの道を行き
今は昔の君ならず
迷いの心は ゆらゆらと
ふらここの 紐のように揺れ動く
角笛の音 寒々と
夜は寂しく過ぎゆきて
夜番の誰何をただ怖れ
涙こらえて装はん
ああ 欺かん 欺かん 欺かん
南宋の寧宗慶元五年(1199)己未、75歳の春、陸游は沈園を再訪しました。40年以上も前に訪れたときには、思いがけずに懐かしい唐婉と出会いましたが、今は知る人もいない。
そんな寂寥の想いと、唐婉の思い出を込めて、陸游は二首の絶句を作りました。
沈園二首 其一 沈園二首 其の一 陸 游
城上斜陽畫角哀 城上の斜陽 畫角哀し
沈園非復旧池台 沈園(しんえん)は復た旧池台に非ず
傷心橋下春波緑 心を傷(いた)ましむ橋下 春波の緑
曾是驚鴻照影來 曾て是れ驚鴻(きやうこう)の影を照(うつし)來る
壁上に夕陽がかたむき 角笛の哀しい音がする
沈園も変わりはて 苑池楼台は見るかげもない
思えば胸が傷んでくる 橋下の池は春にして緑色
鴻のかつて飛び立つ絵姿を 映したこともあったのだ
沈園二首 其二 沈園二首 其の二 陸 游
夢斷香銷四十年 夢は斷え香は銷(き)えて四十年
沈園柳老不飛綿 沈園の柳も老いて綿を飛ばさず
此身行作稽山土 此の身 行々稽山の土と作らんとす
猶弔遺蹤一泫然 猶ほ遺蹤(いしよう)を弔ひて一たび泫然(げんぜん)たり
夢は断ち切られ 余香は消え去って四十年
沈園の柳も老い 柳絮も飛ばなくなった
やがてこの身も 会稽山の土となるだろう
想い出の地を訪れて なおも涙はしとどに流れる 続きを読む
2014年04月16日
奥の細道、いなかの小道(22)− 平泉(2)

芭蕉句碑
(旧暦3月17日)

川端康成(1917)
康成忌
小説家川端康成の昭和47年(1972)の忌日。死因については、自殺説、事故死説がある。
自殺説については、
1. 社会の近代化に伴い、日本から滅びてゆく「もののあはれ」の世界に殉じたという文学的見解
2. 門下とも云うべき三島由紀夫(1925〜1970)の陸上自衛隊東部方面統監部における割腹自決に大きな衝撃を受けたという見解。
3. 創作意欲の減少等、老いへの恐怖などによる強度の精神的動揺や、老醜への恐怖という見解。
など様々に論じられているが、定かではない。
奥の細道、いなかの小道(21)− 平泉(1)のつづき
宝暦十年(1760)三月に上梓された『平泉舊蹟志』の衣川舘の項で相原友直は、「義経は柳御所で自刃し、衣川舘(髙舘)は、奥州藤原氏の政庁平泉館(柳之御所)炎上の時まで民部少輔基成が居住していて火災を遁れた」と述べています。
① 又義經の頼朝卿の勘気をを蒙り下向せし時、秀衡此城の別館に居らしむ、是を柳御所と云けると云ひ傳へり、其趾と云ふは東方にあり、義經は其館に於て自殺せりと云ふ
② 前にも云へる如く衣川館は、泰衡か平泉館炎上の時まで、基成居住し火災を遁れたる事分明なり
義経が衣川舘(髙舘)で自刃したということは、『義経記』以後の伝承によって定説化していますが、『義経記』の作者が高館を最期の地と比定した根拠は、正史である『吾妻鏡』の文治五年閏四月卅日已未の記載によるものではないかと云う説もあります。
源義經研究 源義経終焉の地再考 平泉館と衣河館
http://www.st.rim.or.jp/~success/koromogawanotati_ye.html
日本文化研究家 佐藤弘弥氏
文治五年閏四月卅日已未
今日、於陸奥國、泰衡襲源豫州。是且任勅定、且依二品仰也。豫州在民部少輔基成朝臣衣河舘。泰衡從兵數百騎、馳至其所合戰。豫州家人等雖相防、悉以敗績。豫州入持佛堂、先害妻〔廿二歳〕、子〔女子四歳〕、次自殺云々。
『吾妻鏡』 文治五年
さて、委細はともかく、髙舘に上れば、眼下に北上川が流れ、田畝の向こうに束稲山(たばしねやま)を望むことが出来ます。束稲山は、経塚山、音羽山、束稲山の三つの山の総称で、稲の束がたわんでいるように見えるところから名づけられたとのこと。
束稲山は別名、駒形嶺あるいは駒形山とも云われ、奥州藤原氏が栗駒山(駒ケ岳)山頂にあった陸中国一宮駒形神社(奥州市)の奥宮を度々登拝することに困難を来たすことから、束稲山に駒形大神を奉祀したことに由来しているとされています。
平泉舘下をながれる北上川(來神河)は、三代秀衡の時代、現在よりも東方、駒形山(束稲山)山麓を巡って南流し、櫻川と呼ばれていました。
櫻川
來神河流過平泉舘下川也往時遶駒形山下毎春艶陽之時櫻花一萬株爛慢于峯頂風光漸去飄零日飛此時満川如雪河流變色仍稱之櫻川如今其地為野田尤可慳或指衣關小流者非是
『奥羽観蹟聞老志』 巻之十 磐井郡
櫻川
來神(きたかみ)河流の平泉舘下を過ぐる川也。往時、駒形山(束稲山)下を遶(めぐ)る。毎春艶陽之時、櫻花一萬株、峯頂に爛慢たり。風光漸く去り、飄零日に飛ぶ。此の時満川雪の如く、河流色を變ず。仍(よ)りて之を櫻川と稱す。如今(いま)其の地野田と爲るは、尤も慳(を)しむ可し。或は衣關の小流を指す者、是に非ざるなり。
(嘉穂のフーケモン拙訳)
この駒形山の峯頂に爛慢と咲き誇っていた櫻花一萬株は、その昔、陸奥國奥六郡を治めた俘囚長安倍頼時(生誕不詳〜1057)が、白櫻一萬樹をこの峰に三十余里にわたって植えたので、桜の名所となったと云い伝えられています。
駒形嶺 一称多和枝嶺
在高舘古衣河舘東北以其山在長部村中郷人今曰之長部山斯地往昔安倍頼時植白櫻一萬樹於三十餘里者乃此峯巒也來神河流遶山下與衣河同派西行集所賞多和枝嶺者迺此山也東史曰兼海陸三十余里之間並植櫻樹至四月残雪無消仍號駒形嶺
『奥羽観蹟聞老志』 巻之十 磐井郡
駒形嶺(こまがたね) 一称多和枝嶺(たはしね)
高舘、古(いにしへ)の衣河館の東北に在り。其の山の長部村中に在るを以て、郷人、今は之を長部山と曰ふ。斯の地、往昔(わうせき、いにしえ)、安倍頼時、白櫻一萬樹を三十餘里に植うるは乃ち此の峯巒(ほうがく)也。來神(きたかみ)河山下を遶(めぐ)りて流れ、衣河と同じく派(わか)る。西行、集め賞(ほ)むる處の多和枝嶺(たはしね)は、迺(すなは)ち此の山也。東史(吾妻鏡)に曰く、海陸兼(あはせ)て三十餘里之間、櫻樹を並び植へ、四月に至りて残雪消へること無し。仍(よ)りて駒形嶺と號す。
(嘉穂のフーケモン拙訳)

束稲山
みちの國に、ひらいつみにむかひて、たはしねと申す山の侍るに、こと木はすく
なきやうに、さくらのかきりみえて、花の咲たるをみてよめる
きゝもせすたはしね山のさくら花 よしののほかにかかるへしとは
おくになを人見ぬ花のちらぬあれや 尋ねを入らむ山ほとときす
山家集 西行法師
歌枕として有名な衣川は北上川の支流で、平泉で北上川に注いでいますが、その合流点は、往時は束稲山(駒形峯)山麓であったのが、芭蕉翁訪問時には、髙舘北方約二百メートルの地点に移っていました。
衣河 仙臺より廿三リ半一ノ関、一ノせきより二リ。平泉村ヨリ十四五町行、ヨ程ノ川也。土橋有。南部海道也。今ハ髙舘二十町程間有。古トハ川瀬チガヒシ也。
「名勝備忘録」 曾良
一、衣川、名所なり、此川源二筋あり、北は上衣川村增澤に出、南は淸水大森に出て、同村百袋に至て二川相合し、中尊寺の後を東に流れ、北上川に落つ、衣川
北上川ともに百年前の地圖を以て考合すれば、川筋甚た昔に異なるなり
『平泉舊蹟志』

衣川
題しらす 読人不知
袂より落つる泪はみちのくの 衣川とそいふへかりける
拾遺集 巻十二 戀二 762
義昌
夏たつとしるしも見えず衣川 いつも舟よる浦しなければ
永久百首 夏 138
家隆
誰が袖につゝむほたるの衣川 思ひあまりて玉ともゆらん
夫木抄 巻八 夏二 3229
永承五年十一月後綱朝臣家の歌合水鳥
衣川妻なき鴛(をし)の聲きけは まつ我か袖そさへまさりける
夫木抄 巻十七 冬二 6982
双輪寺にて、松汀にちかしといふことを人々のよみける
西行法師
衣川汀によりて立浪は きしの松か根あらふなりけり
聞書集 全 251
十月十二日、平泉にまかりつきたるけるに、雪降り嵐はげしくことのほかに
あれたりけり、いつしか衣川見まほしくてまかりむかひて見けり、河の岸につ
きて衣川の城しまはしたることからやうかりはりて物を見る心地しにけり、汀
水てとりわけさむければ、
とりわきて心もすみてさへそわたる 衣川見にきたるけふしも
山家集 西行法師
続きを読む
2014年04月11日
奥の細道、いなかの小道(21)− 平泉(1)

奥州藤原氏三代
(旧暦3月12日)
夏草や兵どもが夢の跡
卯の花に兼房みゆる白毛かな 曽良
やっとのことで、奥州平泉にたどり着きました。
かの、藤原三代の栄耀(ええう)、今は見る影もなく、ただ北上川だけが悠然と流れています。
鎌倉時代に成立した歴史書『吾妻鏡』の文治五年八月大廿一日の条にも、当時の荒廃した平泉の有り様が、次のように描かれています。
文治五年八月大廿一日戌申
甚雨暴風。追泰衡、令向岩井郡平泉給
(中略)
泰衡過平泉舘、猶逃亡。縡急而雖融自宅門前、不能暫時逗留。纔遣郎從許件館内、高屋寳藏等縱火。杏梁桂柱之搆、失三代之舊跡。麗金昆玉之貯、爲一時之薪灰。儉存奢失。誠以可愼者哉。
『吾妻鏡』文治五年 己酉
文治五年八月大八日廿一日戌申(ぼしん)
甚雨暴風。泰衡を追て、岩井郡平泉へ向は令(し)め給ふ。
(中略)
泰衡平泉の舘を過ぎ、猶逃亡す。縡(こと)、急にして自宅の門前を融(とほ)ると雖も、暫時も逗留に能はず。纔(わづか)に郎從許りを件(くだん)の館内(たちない)へ遣はし、高屋、寳藏等(ら)に火を縱(はな)つ。杏梁(きやうりやう)桂柱之搆へ、三代之舊跡を失ひ、麗金(れいこん)昆玉之貯(たくは)へ、一時之薪灰(しんかい)と爲す。儉は存し奢は失す。誠に以て愼む可者哉(をや)。
文治五年八月大廿二日己酉
甚雨。申剋、着御于泰衡平泉舘。主者已逐電、家者又化烟。數町之縁邊、寂寞而無人。累跡之郭内、弥滅而有地。只颯々秋風、雖送入幕之響、蕭々夜雨、不聞打窓之聲。但當于坤角、有一宇倉廩。遁餘焔之難。遣葛西三郎淸重、小栗十郎重成等、令見之給。沈、紫檀以下唐木厨子數脚在之。其内所納者、牛玉、犀角、象牙笛、水牛角、紺瑠璃等笏、金沓、玉幡、金花鬘〔以玉餝之〕、蜀江錦直垂、不縫帷、金造鶴、銀造猫、瑠璃燈爐。南廷百〔各盛金器〕等也。其外錦繍綾羅、愚筆不可計記者歟。象牙笛、不縫帷者、則賜淸重、玉幡、金花鬘者、又依重成望申同給之。可庄嚴氏寺之由、申之故也云々。彼瞽叟之牛羊者、雖顯不義之名、此武兵之金玉者、擬備作善之因。財珍係望、古今異事者哉。
『吾妻鏡』文治五年 己酉
文治五年八月大廿二日 己酉(きゆう)
甚雨(豪雨)。申の刻(午後4時前後)、泰衡の平泉の館に着御す。主は已に逐電し、家はまた烟と化す。數町の縁邊、寂寞として人無し。累跡の郭内、いよいよ滅して地のみ有り。ただ颯々(そふそふ)たる秋風、幕に入るの響きを送ると雖も、簫々(せうせう)たる夜雨、窓を打つの聲を聞かず。但し坤(こん、ひつじさる=西南)の角に當り、一宇の倉廩(そうりん)有り。餘焔の難を遁(のが)る。葛西の三郎淸重、小栗の十郎重成等(ら)を遣はし、之を見せ令(し)め給ふ。沈、紫檀以下の唐木の厨子數脚これに在り。その内に納める所は、牛玉、犀角、象牙の笛、水牛の角、紺瑠璃等(ら)の笏、金の沓(くつ)、玉の幡(はた)、金の華鬘(けまん)〔玉を以て之を餝(かざ)る〕、蜀江錦(にしき)の直垂(ひたたれ)、不縫(ぬはず)の帷(かたびら)、金造の鶴、銀造の猫、瑠璃の燈爐、南廷(銀塊)百(各々金の器に盛る)等なり。其の外、錦繍綾羅、愚筆に計(かぞえ)記す可からざる者歟(か)。象牙の笛、不縫(ぬはず)の帷(かたびら)は清重に賜はり、玉の幡(はた)、金の華鬘(けまん)は、また重成望み申すに依て同じく之を給はる。氏寺を荘厳すべきの由、之を申すの故なりと云々。彼の瞽叟(こそう)の牛羊は、不義の名を顯すと雖も、この武兵の金玉は、作善の因に備へんと擬(こら)す。財珍に望みを係るは、古今事を異にする者哉。
奥州平泉文化は、藤原清衡(1056 ?〜1128)、基衡(1106 ?〜1157)、秀衡(1122 ?〜1187)の三代によって築かれました。
われらが先祖みたちの権太郎清衡にこの国の守護を賜はつしよりこのかた、その子に小次郎基衡、いま秀衡まで三代は、国穏やかに治まり、忝くも一天の君の宣旨を蒙り、弓矢の家の名を得しこと、しかしながら当家のご恩たり。
幸若舞 『泉が城』
初代藤原清衡(1056 ?〜1128)は、陸奥国亘理の豪族亘理経清(生年不詳〜1062)と、陸奥国奥六郡(胆沢郡、江刺郡、和賀郡、紫波郡、稗貫郡、岩手郡)を治めた俘囚長安倍頼時(生年不詳〜1057)の娘の有加一乃末陪(あるかいちのまえ)の間の子として生まれ、父の亘理経清が亘理権大夫(わたりのごんのたいふ)を称した関係から、幼名を権太郎と呼ばれたとの説もあるようです。
前九年の役(1051〜1062)で安倍一族が滅亡した後に、母の再婚に従って清原武貞(生没年不詳)の養子となり清原性をとなえますが、後三年の役(1083〜1087)の後、一族最後の残存者として奥六郡を領する勢力者となり、また寬治三年(1089)に陸奥国押領使に任命され、江刺郡豊田に居館を構えました。
寛治五年(1091)、清衡は関白藤原師実(1042〜1101)に馬を献上するなどして京の藤原氏と交誼を深め、この関係より藤原の姓を称するに至ったと言われています。
寬治五年十一月十五日
亥の刻関白殿(師実)の使者来たり曰く、清衡(陸奥の住人なり)、馬二疋進上の由、仰する所也。承りおわんぬ、云々。
『後二条師通記』
嘉保年間(1094〜1096)には磐井郡平泉に居を移し、長治二年(1105)からは中尊寺の中興に着手して壮大な中世都市平泉の原型をつくり、奥州藤原氏三代百年の栄華の基礎を築きました。
二代基衡は毛越寺を再興して京を凌ぐ寝殿造りの金堂と浄土庭園大泉が池を造営し、三代秀衡は無量光院を建立して父祖の業を継承し、嘉応二年(1170)五月二十五日には従五位下鎮守府将軍に叙任され、養和元年(1181)八月二十五日には従五位上陸奥守に叙任されて、名実ともにみちのくの覇者として君臨しました。
一 十三日
天気明。巳ノ尅ヨリ平泉ヘ趣。一リ、山ノ目。壱リ半、平泉ヘ以上弐里半ト云ドモ弐リニ近シ(伊沢八幡壱リ余リ奥也)。高館・衣川・衣ノ関・中尊寺・(別当案内)光堂(金色寺)・泉城・さくら川・さくら山・秀平やしき等ヲ見ル。泉城ヨリ西霧山見ゆルト云ドモ見ヘズ。タツコクガ岩ヤヘ不行。三十町有由。月山・白山ヲ見ル。経堂ハ別當留主ニテ不開。金鶏山見ル。シミン堂、无量劫院跡見、申ノ上尅帰ル。主、水風呂敷ヲシテ待、宿ス。
一 十四日
天気吉。一ノ関(岩井郡之内)ヲ立。
(曾良随行日記)
続きを読む
2014年04月05日
数学セミナー(30)− 調和座標

P. A. M. Dirac an der Tafel
(旧暦3月6日)

達治忌
詩人、翻訳家三好達治の昭和39年(1964)の忌日。
大阪市に生まれ、大阪府立市岡中学を学費が続かず退学後、大阪陸軍地方幼年学校を経て陸軍中央幼年学校本科に入学。大正9年(1920)、陸軍士官学校本科に入学するも翌年、北海道まで脱走して退校処分となった。大正11年(1922)、第三高等学校文科丙類を経て東京帝国大学文学部仏文科を卒業。三高で同級の丸山薫の刺激により詩作を始め、桑原武夫、梶井基次郎、河盛好蔵、吉川幸次郎らを知り、東大では小林秀雄、中島健蔵、今日出海、淀野隆三、堀辰雄らと交友した。
『雪』
十一月の夜をこめて 雪はふる 雪はふる
黄色なランプの灯の洩れる 私の窓にたづね寄る 雪の子供ら
小さな手が玻璃戸を敲く 玻璃戸を敲く 敲く さうしてそこに
息絶える 私は聴く 彼らの歌の 静謐 静謐 静謐
今回も、ディラック先生の『一般相対性理論』の第22章「調和座標」について考えてみませう。
“General Theory of Relativity” P.A.M.DIRAC 22. Harmonic Coordinates
ディラック先生(Paul Adrien Maurice Dirac、1902〜1984)は、イギリスのブリストル大学で電気工学を学んだ後、1923年にケンブリッジのセント・ジョンズ・カレッジ(St John's College)で数学の研究生となりました。
1928年、先生は「フェルミ粒子」を記述するところの「ディラック場」が従う基礎方程式であるディラック方程式を提唱しました。
「フェルミ粒子」(Fermion)とは、スピン角運動量の大きさが (プランク定数 h を 円周率 π の 2 倍で割った量)の半整数 (1/2, 3/2, 5/2, …) 倍の量子力学的粒子であり、その代表は電子になります。そして、その名前の由来は、イタリア=アメリカの物理学者エンリコ・フェルミ (Enrico Fermi、1901〜1954) に依っています。
また、「ディラック場」(Dirac field)とは、スピン角運動量(spin angular momentum)1/2 のフェルミ粒子を記述するスピノル場(Spinor field、整数または半整数のスピンSの粒子を記述している)と定義されています。
ディラック先生は、この方程式から導かれる電子の負のエネルギー状態について、いわゆる「ディラックの海」(Dirac sea)と呼ばれる理論を提案しました。この理論では、電子の電荷と符号が逆で大きさは同じ電荷を持ち、電子と同じ質量を持つ粒子(反粒子)の存在が提起されています。先生は当初、この新粒子を陽子ではないかと考えたようですが、後に電子の反粒子である陽電子が、1932年にアメリカの実験物理学者カール・デイヴィッド・アンダーソン(Carl David Anderson、1905〜1991)によって発見されています。
「ディラックの海」は、相対論的量子論である「ディラック方程式」を解くと出てくる負のエネルギー電子を再解釈して生まれた負のエネルギーで満ちた真空のことですが、光瀬龍原作のSF小説「百億の昼と千億の夜」(萩尾望都により漫画化されている)にも登場しています。
この萩尾望都の漫画が実に印象に残っています。

『アスタータ50惑星開発委員会』が「シ」の命を受けて行う『ヘリオ・セス・ベータ型開発実験』、アトランティスはその一環としてポセイドン神の管理を受けていたが、ポセイドン神の意に逆らったアトランティスはバランスを失い、街の半分を闇にのまれて滅びた。
(中略)
アトランティスの司政官オリオナエ(哲学者プラトンの意識上の分身)は、球体を組み替えて、神のすみか「D座標」に通じる門を作る。その門は、オリハルコンの枠組みに「ディラックの海」のマイナスエネルギーが流れ込み、「D座標」への新しい道を作る装置で、門をくぐった悉達多(シッタータ)、阿修羅、オリオナエの三人は虚数世界に迷いこんでしまう。オリハルコンのかけらがない今、 脱出に失敗すれば「ディラックの海」―完全な無に還元される。
(後略)
The Dirac sea is a theoretical model of the vacuum as an infinite sea of particles with negative energy. It was first postulated by the British physicist Paul Dirac in 1930 to explain the anomalous negative-energy quantum states predicted by the Dirac equation for relativistic electrons. The positron, the antimatter counterpart of the electron, was originally conceived of as a hole in the Dirac sea, well before its experimental discovery in 1932.
( From Wikipedia)
ディラックの海は、負のエネルギーを持った粒子の無限の海として、真空の理論的なモデルである。それはディラック方程式によって相対論的な電子のために予測された異例な負のエネルギーの量子状態を説明するために、1930年にイギリスの物理学者ポール・ディラック(Paul Adrien Maurice Dirac,1902〜1984)により最初に仮定された。電子の反粒子である陽電子は、1932年の実験的な発見の前には、ディラックの海の穴として、当初は考えられた。(Wikipediaより)
ディラック先生は、1933年にオーストリア出身の理論物理学者エルウィン・シュレジンガー(Erwin Rudolf Josef Alexander Schrödinger、1887〜1961)と共に、「新形式の原子理論の発見」(for the discovery of new productive forms of atomic theory)の業績によりノーベル物理学賞を受賞しています。
さて、本題に入ります。
The laws of physics must be valid in all systems of coordinates. They must thus be expressible as tensor equations. Whenever they involve the derivative of a field quantity, it must be a covariant derivative. The field equations of physics must all be rewritten with the ordinary derivatives replaced by covariant derivatives. For example, the d’Alembert equation □V = 0 for a scalar V becomes, in covariant form

This gives, from (10.1) and (10.5)

Even if one is working with flat space (which means neglecting the gravitational field) and one is using curvilinear coordinates, one must write one’s equations in terms of covariant derivatives if one wants them to hold in all systems of coodinates.
“General Theory of Relativity” P.A.M.DIRAC 10. Covariant differentiation
物理法則は、どんな座標系においても、あまねくなりたつのでなければなならい。だから、そのなかに場の量の微分が含まれるとき、それは共変微分でなければならない。物理学における場の方程式は、すべて書きかえて、ふつうの微分を共変微分に直す必要がある。
たとえば、スカラー場に対するダランベールの方程式□V =0の共変な形は、
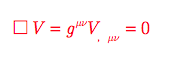
である。これは、(10.1) 、(10.5)により

をあたえる。
たとえ空間を平らだとして(すなわち重力場を無視して)曲線座標をもちいるとしても、方程式が任意の座標系でなりたつようにしたいならば、それは共変微分で書かなくてはいけない。
『一般相対性理論』 P.A.M.ディラック 10.共変微分 (江沢 洋訳)
ちなみに、(10.1) 、(10.5)とは、下記のように式になります。
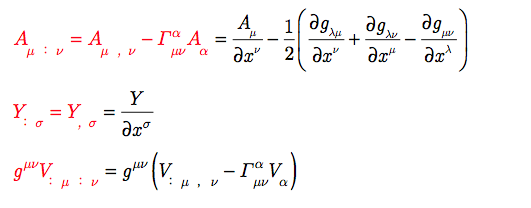
続きを読む



