板橋村だより

　

　マックス・プランク（Max Planck,1858〜1947）　1878年

　（旧暦　 4月 3日）

　四迷忌 　小説家・翻訳家の二葉亭四迷の明治42年（1909）年の忌日。 前年から朝日新聞社特派員としてロシアに渡り、病気で帰国の途中のインド洋上で客死した。

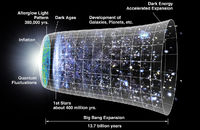
　19世紀の終わりから20世紀の初めにかけて、実験物理学の世界では、それまでの理論では説明できない種々の現象に出くわしていました。

　黒体（外部から入射する、光や電磁波による熱輻射などを、あらゆる波長に渡って完全に吸収する物体で、完全黒体は現実には存在しないと言われていますが、ブラックホールなど近似的にそうみなせる物質、物体はあります）からの熱輻射のスペクトル分布や低温における固体の比熱、あるいは常温での自由な2原子分子の運動において5個の自由度しか現れないということがそのような種類の問題でした。

　ちなみに通常、2原子分子の運動の自由度は、重心の並進運動の自由度3（x方向、y方向、z方向）、重心の周りの回転運動の自由度2（分子軸の回りの回転運動と分子軸に垂直な方向の軸の回りの回転運動）、振動の自由度１の合計6個となります。

　熱輻射の光の波長と強度の関係は温度によって決まることは、19世紀の末に知られるようになりましたが、イギリスの物理学者レーリー（Lord Rayleigh,1842〜1919）とジーンズ（James Hopwood Jeans, 1877〜1946）によって導かれた理論（レーリー・ジーンズの公式）によれば、波長の長い領域で実験結果と一致し、ドイツの物理学者ウィーン（Wilhelm Wien,1864〜1928）によって導かれた理論（ウィーンの法則）では、波長の短い領域で実験結果と一致しました。

　1900年、ドイツの物理学者でベルリン大学教授のマックス・プランク（Max Planck,1858〜1947）は、電磁的輻射の放出・吸収は離散的（連続的ではない）な量子（quanta）として行われると仮定することによって、黒体輻射の問題を説明することができました。
　
　その際、これらの量子（quanta）は、輻射の振動数νに定数h（プランク定数　Planck’s constant）を掛けた分のエネルギーを持つものとされました。
　　 　　　　　
　

　こうして、電磁的輻射の二重の性格すなわち、ある場合には波動のように、また他の場合には粒々の量子の流れのように振る舞うということがはっきりしたものになってきました。

　これはまるで、かつての名優片岡千恵蔵（1903〜1983）演じる探偵「多羅尾伴内」のようではあ〜りませんか。

　「ある時は片目の運転手、ある時は手品好きのキザな紳士、ある時はせむしの怪人、またある時はしがない探偵、しかしてその実体は正義と真実の使徒、藤村大造だっ！」

　あまり脱線しないうちに、今宵はこれまで！

　つづきは、そのうちに。

あなたにおススメの記事